趣味の電子工作などの記録。時にLinuxへ行ったり、ガジェットに浮気したりするので、なかなかまとまらない。
ESP32モジュールと昔買って余っていたグラフィック液晶でNTPで時刻取得する時計を作ってみました。部屋には電波時計があるのですが、鉄筋コンクリートの構造だと全然時刻合わせができませんでした。今だと電波時計よりも無線LAN＋NTPの方が便利かもしれません。ファームウェアはPlatformIOで作ってみました。
今のところは画面は上半分しか使っていませんが、I2Cの端子は空けてあるので、下半分はBME280モジュールを追加して温湿度＋気圧を表示するか、ネットワークの状態を監視して状況を表示するか、そのあたりで考えています。あるいは、アナログっぽい表示にするかもしれません。
それにしても昔の液晶モジュールなので、インタフェースがパラレルで配線本数が多くて大変です。あと、GPIO34以降は入力専用であることに気づかず、表示が出なくてハマりました。
ケースはこれから適当に現物合わせで設計して３Ｄプリンタで出力しようかと思います。
こちらの記事でESP32（など）の開発にとても魅力的な文言が並んでいたので、PlatformIOを試してみました。ちょうど、Visual Studio Codeも試してみたいと思っていたところでもあります。
環境はもちろんいつものLinuxMint19、64bit版です。こちらの手順に沿ってすすめます。
あっという間にインストールが完了しました。１０分もかかってないと思います。
上記画面の右上の「Import Arduino Project」をクリックしてESP32のプロジェクトをインポートしてみます。
ボードはとりあえず、Espressif ESP32 Dev Module を選んでみます。Use libraries installed by Arduino IDEはチェックせず、Arduinoで保存したESP32のNTPのサンプル（SSID/パスワードは記入済）をインポートしてみます。
しばらくすると、インポートが完了しますので、上の方のOpen Projectでインポートしたプロジェクトを開いてみます。
左の方の src にインポートしたソースが表示されるので、これをクリックすると、ソースコードが開きました。’Arduino’ Extension をインストールするよう表示が出るので、Install をクリックしてインストールします。
さらに、.ino ファイルでは何やら支障がある旨表示されて、.cpp に書き換えることが推奨されるので、クリックして表示されるWebページに従って書き換えます。内容としては、
というものです。
下の方の水色のバー（ステータスバーのようなもの）に色々メニューが入っているようです。シェルやシリアルモニタもあります。シリアルモニタを開いたら、「CTRL-T b」で速度を変更できますので、115200に変更しました。
左の方のメニューのPlatform IOアイコン（マウスオンで少し静止するとアイコン名が表示される）をクリックすると、PlatformIOのタスクが表示されるので、Buildをクリックするとコンパイルが実行されます。さらに、Uploadをクリックすると、ファームが書き込まれて実行されました。
書き込み後、シリアルモニタに戻るのですが、設定が元に戻ってしまうようです。
プロジェクトフォルダの中の platformio.ini をこちらに従って書き換えると、初期値を変更できそうです。具体的には、
monitor_speed = 115200
を最後に書き足すだけで大丈夫でした。
確かに簡単に導入できて、便利そうです。
「任意の自然数の各桁を、一桁になるまで掛け算する回数の最大回数とその数を示せ」
という問題で、昨日からCore2 Q6600を動かし続けて電力を消費しまくっています。１３回のパターンが存在しないことは数学的に証明されているらしく、一方で277777788888899が１１回というのは容易に見つかりましたが、そこから先、12回が見つかりません。
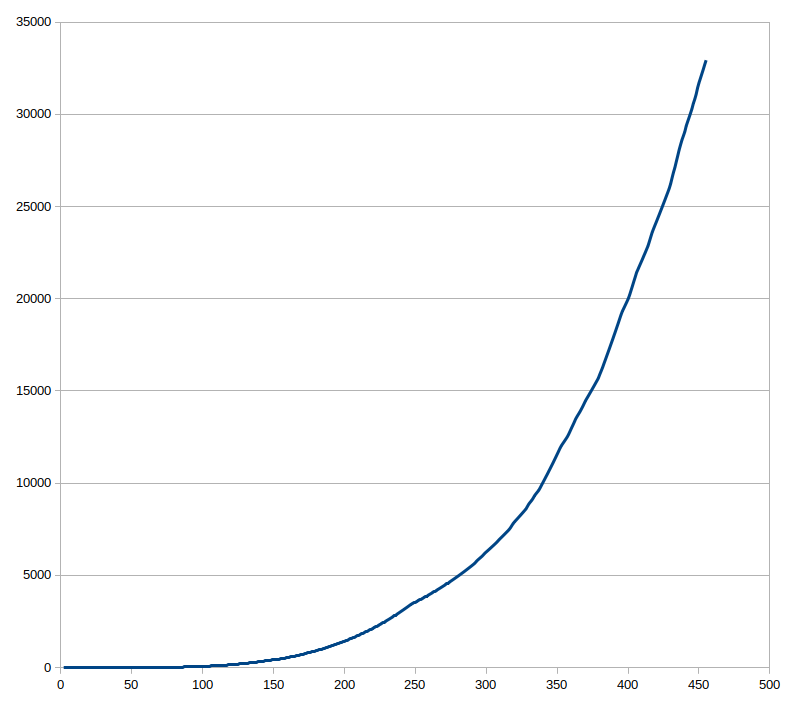
で、高速化の手法を調べているうちに、桁数が多いほど回数が少なくなっていることに気づきました。で、こんなプログラムを作って動かしてみました。（concurrent.futuresを使っていますが、意味はありませんｗ）
import concurrent.futures
def check(m,n):
s = list(str(m**n))
return('0' in s)
def show(k):
r = [i for i in range(1,10001) if not check(k,i)]
print(k,':',r)
if __name__ == "__main__":
kl = [7,8,9]
with concurrent.futures.ProcessPoolExecutor(max_workers=4) as excuter:
result_list = list(excuter.map(show,kl))
結果は、
7 : [1, 2, 3, 6, 7, 10, 11, 19, 35] 8 : [1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27] 9 : [1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34]
こうなりましたが、こんなめんどくさいことしなくても、
>>> [i for i in range(1,10001) if not '0' in list(str(7**i))] [1, 2, 3, 6, 7, 10, 11, 19, 35] >>> [i for i in range(1,10001) if not '0' in list(str(8**i))] [1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27] >>> [i for i in range(1,10001) if not '0' in list(str(9**i))] [1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34] >>>
で十分ですね。
これは、7のみ36個以上（１万個以下）」、8のみ27個以上（１万個以下）、9のみ34個以上（１万個以下）の数値は各桁を乗算すると、出てきた数値の中に０の桁が含まれることを示します。
・・・ということはある桁数以上の検証は無意味かも、と思ったのですが、さらに他の数字をいくつか掛けたときに０の桁が残るかまではわからないのか・・・。
いずれにせよ、桁数がふえると、各桁の乗算結果に０だったり、５と２だったりという桁が出てくる確率が高くなりそうなので、桁数が増えるほど実は回数が少なくなりそうです。
昨日の頭の体操は現在もCore2 Q6600で黙々と処理をしていて、10^617まできましたが、相変わらず12回のパターンはみつかりません。（たぶん、ないのだと思う）
それはさておき concurrent.futures を使用して、複数CPUコアで処理を高速化してみました。他にもちまちまと高速化の工夫を入れました。結果、Core i5-3570K（定格動作）で180桁まで5分かかったのが1分17秒と4倍近く早くなりました。（その過程で、4回のパターンをうまく抽出的できなくなったので誤魔化してあります^^;）
import datetime
import concurrent.futures
keta2 = [2,3,4,5,6,34,35]
def check(n): # 引数の数値が何回かチェックする
k = 1 # ループした回数を保持
t = n # 検査する対象をセット
while True:
u = 1
for i in list(map(int,list(str(t)))) :
u = u * i
if u < 10 :
break
t = u
k += 1
return(k)
def kensho(keta): # その桁数の数値の検証を行う
maxk = 1 # 桁数を保持
maxn = None # 数値を保持
now = datetime.datetime.now()
print("keta: ",keta," / time: ",now-start)
keta789 = keta - 2 #
for s1s2 in ['7'*i+'8'*j+'9'*(keta789-j-i) for i in range(0,keta789+1) for j in range(0,keta789-i+1)] :
for k in keta2: # ２３４５６で構成される数値
s3=str(k)
n = int(s3+s1s2)
r = check(n)
if r > maxk :
maxk = r
maxn = n
# print(keta,maxk,maxn)
return(keta,maxk,maxn)
if __name__ == "__main__":
maxk = 1 # 桁数を保持
maxn = None # 数値を保持
start = datetime.datetime.now()
print('start: ',start)
n = 2
maxlist = {}
while True:
kl = range(n,n+50)
n += 50
with concurrent.futures.ProcessPoolExecutor(max_workers=4) as excuter:
result_list = list(excuter.map(kensho,kl))
# print(result_list)
for k,mk,mn in result_list:
if mk not in maxlist:
maxlist[mk] = mn
elif maxlist[mk] > mn :
maxlist[mk] = mn
print("result")
for i in sorted(maxlist.keys()):
if i>4 : print(i,maxlist[i])
Twitterで見かけた
を考えてみました。
最初はPython3で力ずくで試してみて、９回の34888999まではすぐに見つかりました。しかし、ここからは時間がかかります。傾向をみると、８と９がたくさん含まれる数値ということで、そこにターゲットを絞ってみたところ、277777788888899が１１回というのも比較的短時間でわかりました。１３回のものは存在しないことが証明されているらしいので、残りは１２回のものということになります。
これを効率よく探す方法を考えてみました。
数値の並び順が結果には影響しないのはすぐにわかるので、個々の数値がどんな意味があるか考えてみました。もちろん、探すのは最短桁数のものです。
これらのことから、候補となる数値は７がｘ個、８がｙ個、９がｚ個とそれに付加して２が０〜２個、３が０〜１個、５が０〜１個登場するパターンと思われます。
５は２が０個のときのみ意味があるので、２３５６で構成される桁は最大３桁、４が２ｘ２であることを考えると、２３４５６で構成される最大２桁の範囲で探索すればよいということがわかります。
「２３４５６で構成される最大２桁」＋「７がｘ桁、８がｙ桁、９がｚ桁の組み合わせ」で、２桁の部分をさらに候補を絞ります。２が０〜２桁、３が０〜１桁、５が０〜１桁登場するパターンで、２が２桁＝４が１桁であることを考えると、２が１桁＝２、２が２桁＝２２＝４と同じ、３が１桁＝３、５が１桁＝５、２が１桁＋３が１桁＝６と同じ、２が２桁＋３が１桁＝３４と同じ、３が１桁＋５が１桁＝３５と同じ、ということから、探索するのは[２，４，３，５，６，３４，３５］だけで良いと思われます。
そこで、[２，４，３，５，６，３４，３５］＋（７，８，９の組み合わせからなる多数桁）をチェックするPython3プログラムを作成しました。（見直すと、もっときれいに書けそうですが・・・）
import datetime
keta2 = [2,3,4,5,6,34,35]
maxk = 1 # 桁数を保持
maxn = None # 数値を保持
def once(n): # １回の計算を行う
t = 1
for i in list(str(n)) :
t = t * int(i)
return(t)
def check(n): # 引数の数値が何回かチェックする
global maxk,maxn
k = 1 # ループした回数を保持
t = n # 検査する対象をセット
while True:
r = once(t)
if r < 10 :
break
t = r
k += 1
if k == maxk :
print('同等 ',n,k)
if k > maxk :
maxk = k
maxn = n
print('更新 ',n,k)
def check_print(n): # 引数の数値が何回か出力しながらチェックする
global maxk,maxn
k = 1 # ループした回数を保持
t = n # 検査する対象をセット
while True:
r = once(t)
if r < 10 :
break
t = r
k += 1
print(t,' ',end='')
def kensho(keta): # その桁数の数値の検証を行う
keta789 = keta - 2 #
for i in range(0,keta789+1):
s1 = '7'*i
keta89 = keta789 - i;
for j in range(0,keta89+1):
s2 = '8'*j + '9'*(keta89-j)
for k in keta2: # ２３４５６で構成される数値
s3=str(k)
n = int(s3+s1+s2)
check(n)
if __name__ == "__main__":
start = datetime.datetime.now()
print('start: ',start)
# for keta in range(2,100+1) :
keta = 2
while True:
now = datetime.datetime.now()
print("keta: ",keta," / time: ",now-start," / record: ",maxn,maxk)
kensho(keta)
keta += 1
print("result ",maxn,maxk)
check_print(maxn)
これを Core2 Q6600（古い・・）で実行すると、
keta: 2 / time: 0:00:00.000048 / record: None 1 同等 2 1 同等 3 1 同等 4 1 同等 5 1 同等 6 1 更新 34 2 同等 35 2 keta: 3 / time: 0:00:00.000200 / record: 34 2 同等 29 2 更新 39 3 同等 49 3 同等 59 3 同等 69 3 同等 359 3 同等 68 3 更新 348 4 keta: 4 / time: 0:00:00.000449 / record: 348 4 同等 699 4 同等 3499 4 同等 489 4 同等 3489 4 更新 688 5 同等 3488 5 同等 679 5 keta: 5 / time: 0:00:00.000870 / record: 688 5 同等 6999 5 同等 34999 5 同等 34888 5 更新 6788 6 keta: 6 / time: 0:00:00.001480 / record: 6788 6 同等 49999 6 更新 68889 7 同等 347799 7 keta: 7 / time: 0:00:00.002459 / record: 68889 7 同等 377889 7 更新 3477889 8 keta: 8 / time: 0:00:00.003920 / record: 3477889 8 同等 6999999 8 同等 6888999 8 更新 34888999 9 keta: 9 / time: 0:00:00.005924 / record: 34888999 9 keta: 10 / time: 0:00:00.008575 / record: 34888999 9 keta: 11 / time: 0:00:00.011963 / record: 34888999 9 更新 3778888999 10 keta: 12 / time: 0:00:00.016466 / record: 3778888999 10 keta: 13 / time: 0:00:00.022207 / record: 3778888999 10 keta: 14 / time: 0:00:00.029282 / record: 3778888999 10 同等 3888888888889 10 keta: 15 / time: 0:00:00.037926 / record: 3778888999 10 keta: 16 / time: 0:00:00.048363 / record: 3778888999 10 更新 277777788888899 11 keta: 17 / time: 0:00:00.060824 / record: 277777788888899 11 keta: 18 / time: 0:00:00.075424 / record: 277777788888899 11 同等 27777789999999999 11 keta: 19 / time: 0:00:00.092772 / record: 277777788888899 11 keta: 20 / time: 0:00:00.112918 / record: 277777788888899 11
ということで、60msほどで11回のものまで見つかりました。
これをひたすら回して、現在１１時間で470桁くらいまで到達しているのですが、今の所１２回のパターンは見つかっていません。横軸に桁数、縦軸にその桁数までの所要時間（秒）を取ると、
という感じで、概ね所要時間は ７．７×桁数^4×10^(-7) （秒）で近似できそうです。となると、１０００桁までチェックすると９日くらいかかりそうです。
PIC12F1822でLチカしたときの消費電流を測ってみました。どのくらい消費電流が抑えられるか（＝どのくらい電池動作ができるか）を確認したいので。
レジスタの設定はすべてCode Cofiguratorにお任せ。
CPUのクロックは初期設定の500kHzです。
特にあれこれ設定はいじらず、TMR1でぼんやり明滅するタイミング（100ms周期）を生成、割り込みを発生させて、PWM2のデューティーを変動させます。TMR2は100us周期のクロックを生成して、ECCPでPWM波形を生成します。そして、PWM端子の出力に１ｋΩを通して高輝度LEDを接続して点灯させます。なお、不要な端子は入力端子として、貫通電流による消費電力増加を防ぐため内部プルアップを有効化してあります。
作成したソースコードは main.c の以下の部分だけです。見ての通り、初期化以外はすべて100msに１回の割り込みの際に処理しています。
#include "mcc_generated_files/mcc.h"
uint8_t c=0;
uint16_t pwmt[]={
0, 2, 4, 6, 8,10,12,14,16,18,
20,20,20,20,20,20,20,20,20,20,
18,16,14,12,10, 8, 6, 4, 2, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0
};
void TMR1int(void){
c++;
if(c == sizeof(pwmt)/sizeof(uint16_t)) c=0;
EPWM_LoadDutyValue(pwmt[c]);
}
void main(void)
{
SYSTEM_Initialize();
TMR1_SetInterruptHandler(TMR1int);
INTERRUPT_GlobalInterruptEnable();
INTERRUPT_PeripheralInterruptEnable();
while (1)
{
// Add your application code
}
}
単４電池２本で動かしてみると、消費電流は平均で0.2mA〜0.6mAなので、こちらの資料を参考にすると2,900時間くらい持つ計算です。つまり、約４ヶ月くらいでしょうか。ただ、電圧が落ちてくるとLEDが点灯しなくなる可能性があるので、実際にはそんなに持たないかもしれませんが。
＜追伸＞
ソースコードの中の EPWM_LoadDutyValue(pwmt) という部分は、実際には EPWM_LoadDutyValue(pwmt［c］)です。SyntaxHighlighter を使っているのですが、半角の［c］がタグとして扱われるのか、消えてしまいます。orz
３Ｄプリンタ用保温ボックスを作って、ABSでの出力がうまく行くようになったのはいいのですが、ボックス内がかなり高温になっている（あたりまえですが・・・）のが気になります。
実際どのくらいなのか、手持ちの部品で温度を測ってみることにしました。
PCへの取り込みはシリアルで、秋月で以前購入したFTDI USBシリアル変換ケーブル（５V）を使いました。マイコンはPIC12F1822、温度センサーはLM35DZを使っています。最初はESP8266かESP32でAmbientに直接送信させようかとも思ったのですが、今回は測定気温が80℃を超えているかもしれませんし、場合によっては100℃を超えているかもしれません。なので、自己発熱が少なく（＝消費電力を抑えることができる）壊れてもすぐ交換可能なPICとデータシート上150℃まで動作可能なLM35を使用することにしました。
ソフトはMPLAB Code Configuratorで以下のように設定しました。
これでMPLAB Code Configuratorにソースを吐かせて、main.cを作成しました。
#include "mcc_generated_files/mcc.h"
#include <stdlib.h>
bool exec=false;
unsigned long int time=0;
void TMR1int(void){
exec = true;
time++;
}
/*
Main application
*/
inline void EUSART_putchar(unsigned char ch){
EUSART_Write(ch);
}
void EUSART_puts(char *str){
uint16_t p=0;
while(str[p]!=0) EUSART_putchar(str[p++]); // Write data
}
void EUSART_putdec(unsigned long int num){
char buf[10];
unsigned long int t,u;
int8_t i=0;
while(1){
buf[i]=(num % 10)+'0';
num = num / 10;
if(num == 0)break;
i++;
}
while(i>=0){
EUSART_putchar(buf[i]);
i--;
}
}
void EUSART_putLM35(unsigned long int num){
char buf[10];
unsigned long int t,u;
int8_t i=0;
while(1){
buf[i]=(num % 10)+'0';
num = num / 10;
if(num == 0)break;
i++;
}
while(i>=0){
if(i==0) EUSART_putchar('.');
EUSART_putchar(buf[i]);
i--;
}
}
void main(void)
{
// initialize the device
SYSTEM_Initialize();
// EUSART_Initialize();
TMR1_SetInterruptHandler(TMR1int);
exec = false;
time=0;
// Enable the Global Interrupts
INTERRUPT_GlobalInterruptEnable();
// Enable the Peripheral Interrupts
INTERRUPT_PeripheralInterruptEnable();
while (1)
{
if(exec){
// Read LM35DZ
uint16_t convertedValue;
ADC_Initialize();
convertedValue = ADC_GetConversion(channel_AN2);
// Send to HOST
EUSART_putdec(time);
EUSART_putchar(' ');
EUSART_putLM35((unsigned long int)convertedValue);
EUSART_putchar(0x0d);
EUSART_putchar(0x0a);
exec = false;
}
// Add your application code
}
}
ビルドして、PICkit3で書き込みます。書き込む際はICクリップを使うことで、基板上の書き込みに関する信号の配線作業を省略しています。DIPパッケージで２０ピンまでの8bitのPICは電源/GNDを含めて１ピン側の８ピンに書き込みに必要な信号が共通で出ています。ですので、この８ピンのICクリップは２０ピンまでの８ビットのPICで共通に使用することができます。（例外はあるかもしれませんが・・・）
実行すると１秒単位に電源投入からの経過秒数と温度を出力します。
: : 898 29.7 899 29.8 900 29.6 901 29.7 902 29.6 903 29.7 904 29.6 905 29.8 906 29.7
測定したら、そのテキストファイルをLibre Officeに読み込ませてグラフ化させるつもりです。
3D Benchyの出力風景です。
ABSのデフォルト設定のノズル温度 230℃、ベッド温度 80℃、ファン 100%、積層ピッチ 0.15mmだと１～２ｍｍ出力したところでベッドから剥がれてしまったのですが、ノズル温度 240℃、ベッド温度 100℃、ファン 60%、積層ピッチ 0.15mmだと最後まで剥がれずに出力できました。
しかし、かなり保温ボックスの中の温度が上がっているので、いったい何度になっているのかチェックしておかないと危険かもしれません。
以前試してみて全然ダメだったABSでの出力ですが、あきらめきれないので再度試してみました。
今度は、MDFとプラ段で保温ボックスを作ってみました。
底板はMDFで、側面と天板はクリアのプラ段で、結合は白色の養生テープで行っています。
MDFは２枚重ねて底に敷いています。寸法を4mm差をつけることにより、ここにプラ段を載せています。本当はプラ段は前面用、背面用は488mm×484mmにするべきだったかもしれません。
プラ段はクリアを使うことにより外につけたLEDライトの光が中に入るので作業性の悪化は避けることができました。また、以前設置したTTGO T-Cameraもそのまま使うことができました。
ちょっとファンのカバーが白のせいで白飛び気味なので、ファンカバーを黒で作り直した方がよさそうですが。
写真はスプールにつけるホルダー用の柱をPLAで出力しているところですが、２００℃／６０℃でも内部はすごい熱気です。これで電源ユニットやコントローラが耐えられるのか心配ですので、今度温度計を放り込んでみます。
肝心のABSでの出力ですが、ノズル２３０℃、ベッド８０℃では途中でベッドから剥がれてしまいます。現在、ノズル２４０℃、ベッド１００℃、ファン速度６０％でトライ中です。
内部はさらに熱気が高まると思いますので、その対策が必要かもしれません。