Twitterで見かけた
を考えてみました。
最初はPython3で力ずくで試してみて、9回の34888999まではすぐに見つかりました。しかし、ここからは時間がかかります。傾向をみると、8と9がたくさん含まれる数値ということで、そこにターゲットを絞ってみたところ、277777788888899が11回というのも比較的短時間でわかりました。13回のものは存在しないことが証明されているらしいので、残りは12回のものということになります。
これを効率よく探す方法を考えてみました。
数値の並び順が結果には影響しないのはすぐにわかるので、個々の数値がどんな意味があるか考えてみました。もちろん、探すのは最短桁数のものです。
- 0は乗算するといきなり0になってしまうので、候補になりえません。
- 1は桁数を増やす効果しかないので、最小桁数のものを考える上では探索不要です。
- 4は2x2、6は2x3、8は2x2x2、9は3x3なので、桁数を短縮する効果があります。
- 7は素数ですから、桁数を短縮する効果はありません。
- 5は2が出てこないケースにおいてのみ意味があります。2があると、結果に0が含まれてしまい、2回で終わってしまいます。
- 2と3は素数ですから、これ以上桁数を短縮する効果はありません。
これらのことから、候補となる数値は7がx個、8がy個、9がz個とそれに付加して2が0〜2個、3が0〜1個、5が0〜1個登場するパターンと思われます。
5は2が0個のときのみ意味があるので、2356で構成される桁は最大3桁、4が2x2であることを考えると、23456で構成される最大2桁の範囲で探索すればよいということがわかります。
「23456で構成される最大2桁」+「7がx桁、8がy桁、9がz桁の組み合わせ」で、2桁の部分をさらに候補を絞ります。2が0〜2桁、3が0〜1桁、5が0〜1桁登場するパターンで、2が2桁=4が1桁であることを考えると、2が1桁=2、2が2桁=22=4と同じ、3が1桁=3、5が1桁=5、2が1桁+3が1桁=6と同じ、2が2桁+3が1桁=34と同じ、3が1桁+5が1桁=35と同じ、ということから、探索するのは[2,4,3,5,6,34,35]だけで良いと思われます。
そこで、[2,4,3,5,6,34,35]+(7,8,9の組み合わせからなる多数桁)をチェックするPython3プログラムを作成しました。(見直すと、もっときれいに書けそうですが・・・)
import datetime
keta2 = [2,3,4,5,6,34,35]
maxk = 1 # 桁数を保持
maxn = None # 数値を保持
def once(n): # 1回の計算を行う
t = 1
for i in list(str(n)) :
t = t * int(i)
return(t)
def check(n): # 引数の数値が何回かチェックする
global maxk,maxn
k = 1 # ループした回数を保持
t = n # 検査する対象をセット
while True:
r = once(t)
if r < 10 :
break
t = r
k += 1
if k == maxk :
print('同等 ',n,k)
if k > maxk :
maxk = k
maxn = n
print('更新 ',n,k)
def check_print(n): # 引数の数値が何回か出力しながらチェックする
global maxk,maxn
k = 1 # ループした回数を保持
t = n # 検査する対象をセット
while True:
r = once(t)
if r < 10 :
break
t = r
k += 1
print(t,' ',end='')
def kensho(keta): # その桁数の数値の検証を行う
keta789 = keta - 2 #
for i in range(0,keta789+1):
s1 = '7'*i
keta89 = keta789 - i;
for j in range(0,keta89+1):
s2 = '8'*j + '9'*(keta89-j)
for k in keta2: # 23456で構成される数値
s3=str(k)
n = int(s3+s1+s2)
check(n)
if __name__ == "__main__":
start = datetime.datetime.now()
print('start: ',start)
# for keta in range(2,100+1) :
keta = 2
while True:
now = datetime.datetime.now()
print("keta: ",keta," / time: ",now-start," / record: ",maxn,maxk)
kensho(keta)
keta += 1
print("result ",maxn,maxk)
check_print(maxn)
これを Core2 Q6600(古い・・)で実行すると、
keta: 2 / time: 0:00:00.000048 / record: None 1 同等 2 1 同等 3 1 同等 4 1 同等 5 1 同等 6 1 更新 34 2 同等 35 2 keta: 3 / time: 0:00:00.000200 / record: 34 2 同等 29 2 更新 39 3 同等 49 3 同等 59 3 同等 69 3 同等 359 3 同等 68 3 更新 348 4 keta: 4 / time: 0:00:00.000449 / record: 348 4 同等 699 4 同等 3499 4 同等 489 4 同等 3489 4 更新 688 5 同等 3488 5 同等 679 5 keta: 5 / time: 0:00:00.000870 / record: 688 5 同等 6999 5 同等 34999 5 同等 34888 5 更新 6788 6 keta: 6 / time: 0:00:00.001480 / record: 6788 6 同等 49999 6 更新 68889 7 同等 347799 7 keta: 7 / time: 0:00:00.002459 / record: 68889 7 同等 377889 7 更新 3477889 8 keta: 8 / time: 0:00:00.003920 / record: 3477889 8 同等 6999999 8 同等 6888999 8 更新 34888999 9 keta: 9 / time: 0:00:00.005924 / record: 34888999 9 keta: 10 / time: 0:00:00.008575 / record: 34888999 9 keta: 11 / time: 0:00:00.011963 / record: 34888999 9 更新 3778888999 10 keta: 12 / time: 0:00:00.016466 / record: 3778888999 10 keta: 13 / time: 0:00:00.022207 / record: 3778888999 10 keta: 14 / time: 0:00:00.029282 / record: 3778888999 10 同等 3888888888889 10 keta: 15 / time: 0:00:00.037926 / record: 3778888999 10 keta: 16 / time: 0:00:00.048363 / record: 3778888999 10 更新 277777788888899 11 keta: 17 / time: 0:00:00.060824 / record: 277777788888899 11 keta: 18 / time: 0:00:00.075424 / record: 277777788888899 11 同等 27777789999999999 11 keta: 19 / time: 0:00:00.092772 / record: 277777788888899 11 keta: 20 / time: 0:00:00.112918 / record: 277777788888899 11
ということで、60msほどで11回のものまで見つかりました。
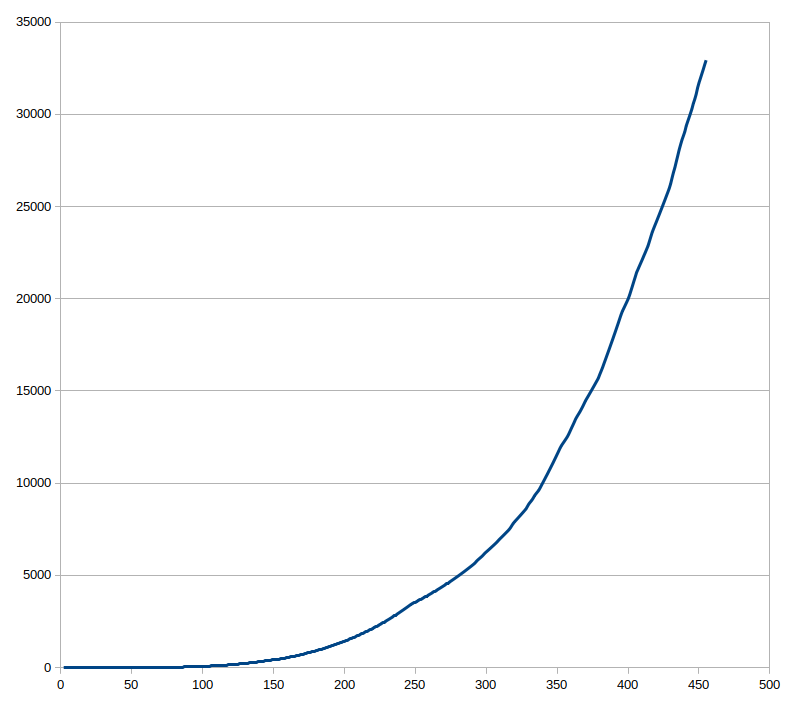
これをひたすら回して、現在11時間で470桁くらいまで到達しているのですが、今の所12回のパターンは見つかっていません。横軸に桁数、縦軸にその桁数までの所要時間(秒)を取ると、
という感じで、概ね所要時間は 7.7×桁数^4×10^(-7) (秒)で近似できそうです。となると、1000桁までチェックすると9日くらいかかりそうです。